

 Python Tutorials Python Tutorials | (back to the list of tutorials) |
 Accessing X, Y and Z of Vector
Accessing X, Y and Z of Vector![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
vec = IVec(20, 10, 0)
xvalue = vec.x()
print("x value is " + str(xvalue) )
yvalue = vec.y()
print("y value is " + str(yvalue) )
zvalue = vec.z()
print("z value is " + str(zvalue) )

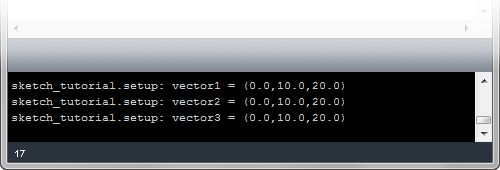
 Duplicate Vectors
Duplicate Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(0, 10, 20)
v2 = v1.dup()
# v2 = v1.cp() # cp() is alias of dup()
v3 = IVec(v1)
print("vector1 = " + str(v1) )
print("vector2 = " + str(v2) )
print("vector3 = " + str(v3) )
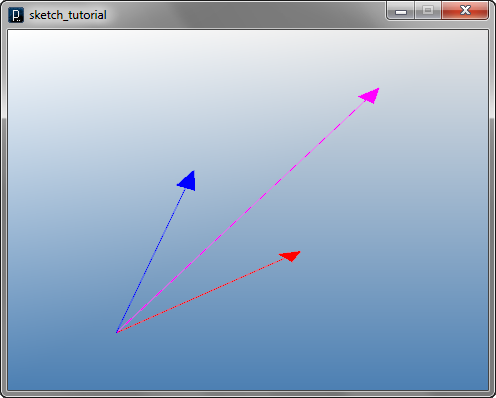
 Add/Subtract Vectors
Add/Subtract Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
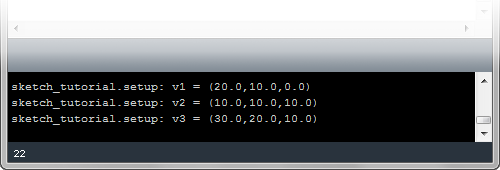
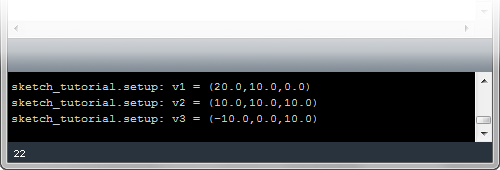
v1 = IVec(20, 10, 0)
v2 = IVec(10, 10, 10)
v3 = v2.dup()
v3.add(v1)
# visualizing vectors as arrows
v1.show().clr(1.,0,0) # red
v2.show().clr(0,0,1.) # blue
v3.show().clr(1.,0,1.) # magenta
print("v1 = " + str(v1) )
print("v2 = " + str(v2) )
print("v3 = " + str(v3) )
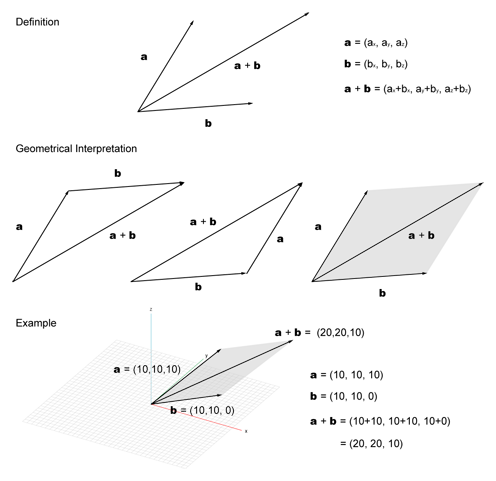
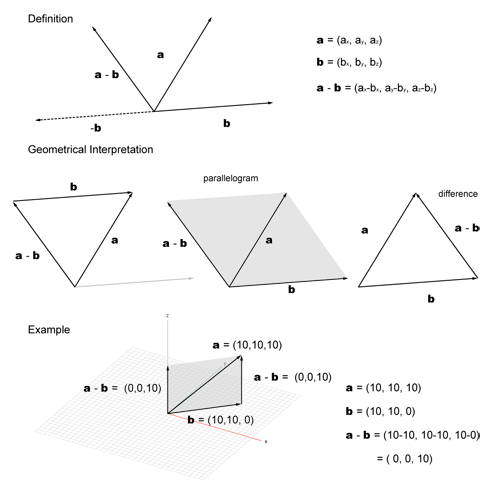
Mathematical meaning of vector addition is like the following diagram.
Subtracting vectors is done in the same way with adding.
Please use sub() method.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
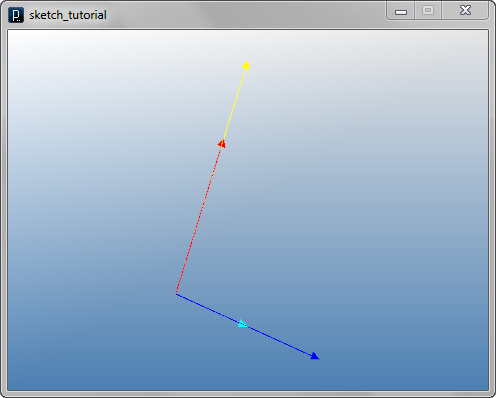
v1 = IVec(20, 10, 0)
v2 = IVec(10, 10, 10)
v3 = v2.dup()
v3.sub(v1)
# visualizing vectors as arrows
v1.show().clr(1.,0,0) # red
v2.show().clr(0,0,1.) # blue
v3.show().clr(1.,0,1.) # magenta
print("v1 = " + str(v1) )
print("v2 = " + str(v2) )
print("v3 = " + str(v3) )

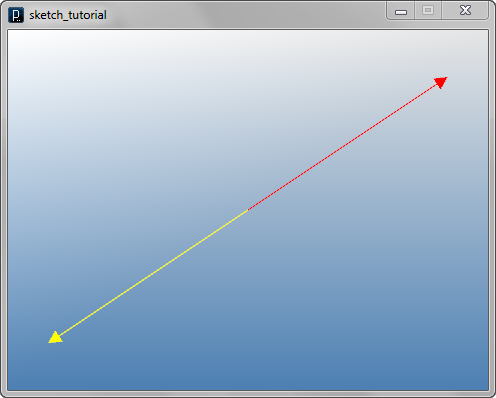
Vector subtraction can be diagrammed like the below.
 Multiply/Divide Vectors
Multiply/Divide Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10, 20, 30)
v2 = v1.dup()
v2.mul(1.5)
v3 = IVec(30, -10, -10)
v4 = v3.dup()
v4.div(2.0)
v1.show().clr(1.,0,0) # red
v2.show().clr(1.,1.,0) # yellow
v3.show().clr(0,0,1.) # blue
v4.show().clr(0,1.,1.) # cyan
print("v1 = " + str(v1) )
print("v2 = " + str(v2) )
print("v3 = " + str(v3) )
print("v4 = " + str(v4) )

Vector multiplication can be described like the below. Vector division can be seen as multiplication of inverted scalar number.

 Flip Vectors
Flip Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(30, 20, 10)
v2 = v1.dup()
v2.flip()
v1.show().clr(1.,0,0) # red
v2.show().clr(1.,1.,0) # yellow
print("v1 = " + str(v1) )
print("v2 = " + str(v2) )
 Length, Distance and Unitization
Length, Distance and Unitization![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
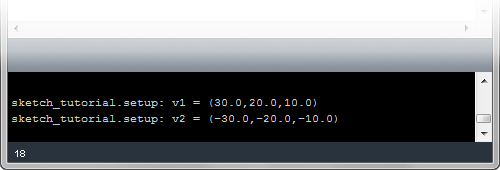
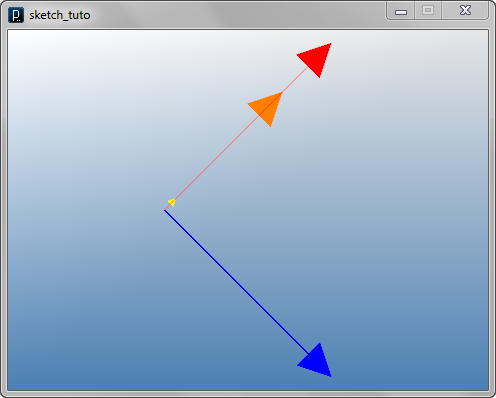
v1 = IVec(10,10,0)
length = v1.len()
v2 = IVec(10,-10,0)
distance = v1.dist(v2)
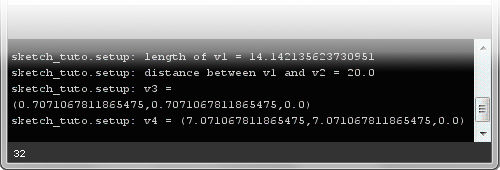
v3 = v1.dup()
v3.unit()
v4 = v1.dup()
v4.len(10)
v1.show().clr(1.,0,0) #red
v2.show().clr(0,0,1.) #blue
v3.show().clr(1.,1.,0).size(0.5) #yellow w head size 0.5
v4.show().clr(1.,.5,0) #orange
print("length of v1 = " + str(length) )
print("distance between v1 and v2 = " + str(distance) )
print("v3 = " + str(v3) )
print("v4 = " + str(v4) )
Those operations can also be described as the following.

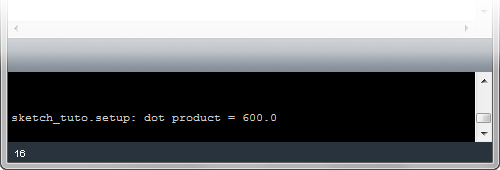
 Dot Product
Dot Product
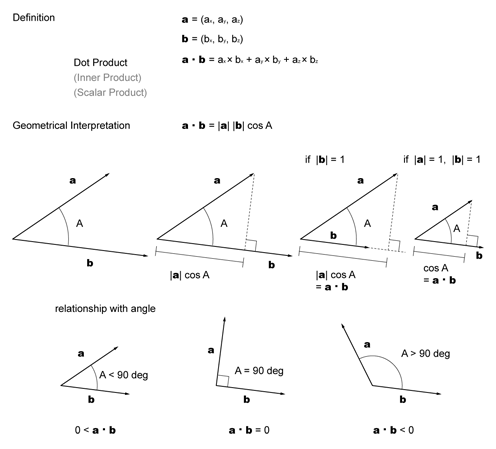
In IVec class, you can use dot() method with another vector put in the argument. Please note that dot() method is returning a value in double, not a vector.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10,20,30)
v2 = IVec(10,10,10)
dotValue = v1.dot(v2) # result is a floating point number, not a vector
print("dot product = " + str(dotValue) )
 Cross Product
Cross Product
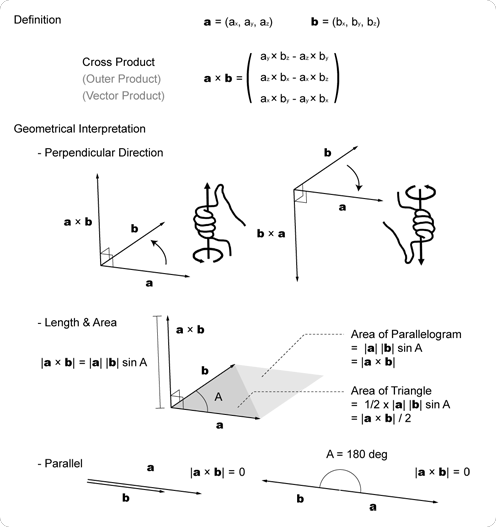
In iGeo, you can calculate a cross product by cross() with another vector put in the argument. Please note that cross() generates a new vector, without changing the contents of itself. which is different behavior from add/sub/mul/div where the result of the method is contained inside the one of input vectors changing its contents.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10, 20, 30)
v2 = IVec(5, 20, 10)
v3 = v1.cross(v2)
v1.show().clr(1.,0,0)
v2.show().clr(0,0,1.)
v3.show().clr(1.,1.,0)

 Angle and Rotation
Angle and Rotation![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(0, 10, 10)
v2 = IVec(0, -5, 5)
axisVec = IVec(1, 0, 0)
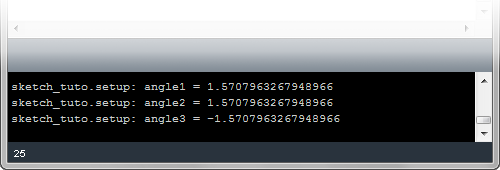
angle1 = v1.angle(v2)
angle2 = v1.angle(v2, axisVec)
angle3 = v2.angle(v1, axisVec)
print("angle1 = " + str(angle1) )
print("angle2 = " + str(angle2) )
print("angle3 = " + str(angle3) )
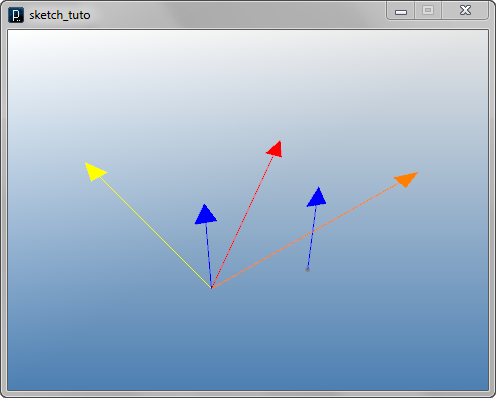
To rotate a vector, you use rot() method. There are two different types of arguments. In the first one, you put an axis vector in the first argument and angle in the second argument as a double value (the unit is in radian). The second type of the argument is that you put a center point of rotation as IVec in the first argument and the second is an axis vector and the third is rotation angle.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10, 10, 10)
axis = IVec(0, 0, 10)
v2 = v1.dup()
v2.rot(axis, PI/2)
center = IVec(10,0,0)
v3 = v1.dup()
v3.rot(center, axis, -PI/2)
v1.show().clr(1.,0,0)
axis.show().clr(0,0,1.)
v2.show().clr(1.,1.,0)
centerPt = IPoint(center)
axis.show(center).clr(0,0,1.)
v3.show().clr(1.,.5,0)
 Reflect Vectors
Reflect Vectors
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10,10,10)
planeNormal = IVec(10,0,0)
v2 = v1.dup()
v2.ref(planeNormal)
planeCenter = IVec(20,0,0);
v3 = v1.dup()
v3.ref(planeCenter, planeNormal)
v1.show().clr(1.,0,0)
planeNormal.show().clr(0,0,1.)
v2.show().clr(1.,1.,0)
IPoint(planeCenter)
planeNormal.show(planeCenter).clr(0,0,1.)
v3.show().clr(1.,.5,0)

 Compare Vectors
Compare Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(70, 20, 90)
v2 = IVec(50, 50, 40)
for i in range(10) :
for j in range(10) :
for k in range(10) :
v = IVec(i*10, j*10, k*10)
if v.eq(v1) :
IPoint(v).clr(1.,.8,1.)
elif v.eq(v2, 30) :
IPoint(v).clr(1.,0,0)
else :
IPoint(v)

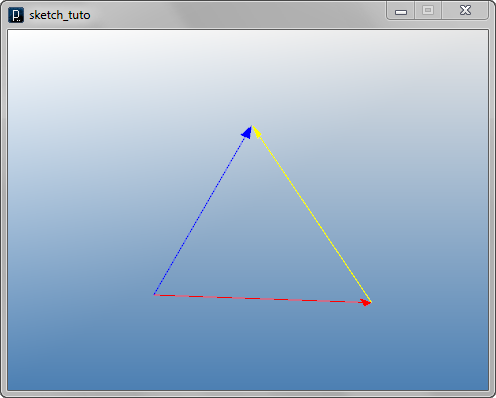
 Create Difference Vectors
Create Difference Vectors
IVec v3 = v2.dif(v1);
IVec v3 = v2.dup().sub(v1);
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(30,-20,-10)
v2 = IVec(20,0,20)
v3 = v2.dif(v1)
v1.show().clr(1.,0,0)
v2.show().clr(0,0,1.)
v3.show(v1).clr(1.,1.,0)
 Create Midpoint/Bisector Vectors
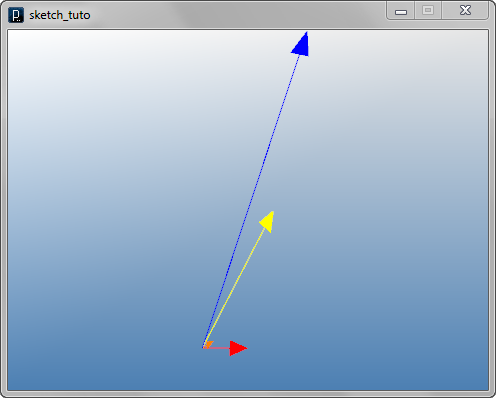
Create Midpoint/Bisector Vectors
IVec v3 = v1.mid(v2);
IVec v3 = v1.dup().add(v2).div(2);
IVec v4 = v1.bisect(v2);
IVec v4 = v1.dup().unit().add(v2.dup().unit());
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(10,0,0)
v2 = IVec(10,10,10)
v3 = v1.mid(v2)
v4 = v1.bisect(v2)
v1.show().clr(1.,0,0)
v2.show().clr(0,0,1.)
v3.show().clr(1.,1.,0)
v4.show().clr(1.,.5,0).size(1) # making a head small
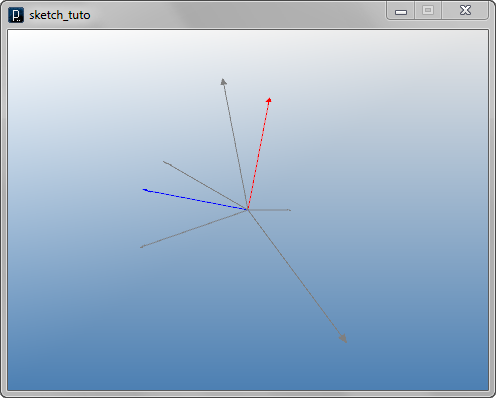
 Create Summation Vectors
Create Summation Vectors![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(20,0,-10)
v2 = IVec(10,20,30)
total1 = v1.sum(v2) # sum of two vectors
v3 = IVec(-20,30,-20)
v4 = IVec(-30,-10,30)
v5 = IVec(-10,-40,-10)
total2 = v1.sum(v2,v3,v4,v5) # sum of five vectors
v1.show()
v2.show()
v3.show()
v4.show()
v5.show()
total1.show().clr(1.,0,0)
total2.show().clr(0,0,1.)
 Create Weighted Summation Vectors
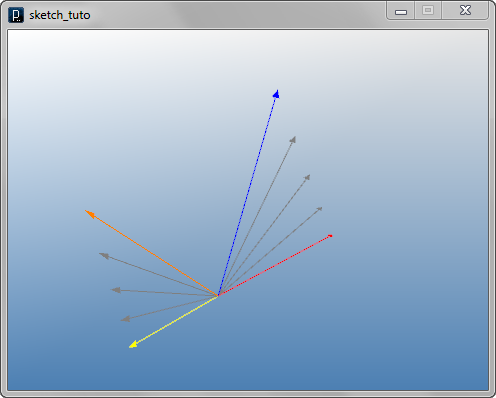
Create Weighted Summation Vectors
IVec v3 = v1.sum(v2, 0.2, 0.8);
IVec v3 = v1.dup().mul(0.2).add(v2.dup().mul(0.8));
IVec v4 = v1.sum(v2, 0.8);
IVec v4 = v1.dup().mul(1-0.8).add(v2.dup().mul(0.8));
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
v1 = IVec(50,0,-10)
v2 = IVec(30,10,40)
u1 = v1.sum(v2, 0.75, 0.25)
u2 = v1.sum(v2, 0.5, 0.5)
u3 = v1.sum(v2, 0.25, 0.75)
v3 = IVec(-20,10,-10)
v4 = IVec(-20,10,30)
u4 = v3.sum(v4, 0.25)
u5 = v3.sum(v4, 0.5)
u6 = v3.sum(v4, 0.75)
v1.show().clr(1.,0,0)
v2.show().clr(0,0,1.)
v3.show().clr(1.,1.,0)
v4.show().clr(1.,.5,0)
u1.show()
u2.show()
u3.show()
u4.show()
u5.show()
u6.show()
 HOME
HOME
 FOR PROCESSING
FOR PROCESSING
 DOWNLOAD
DOWNLOAD
 DOCUMENTS
DOCUMENTS
 TUTORIALS (Java /
Python)
TUTORIALS (Java /
Python)
 GALLERY
GALLERY
 SOURCE CODE(GitHub)
SOURCE CODE(GitHub)
 PRIVACY POLICY
PRIVACY POLICY
 ABOUT/CONTACT
ABOUT/CONTACT
