
 Python Tutorials Python Tutorials | (back to the list of tutorials) |
 Mathematics of NURBS Geometry
Mathematics of NURBS Geometry
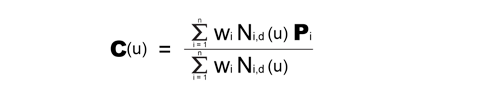
Similarly, a NURBS surface is defined by the formula below, where now control points Pi,j and weights wi,j are provided as n x m matrix. This is a function of two parameters u and v and it returns spatial coordinates corresponding to the input u and v.
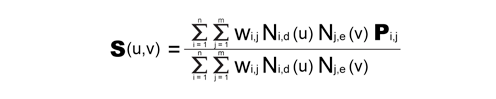
For more detail description of NURBS geometries and basis functions, see Wikipedia pages of NURBS, B-Spline and Bernstein Polynomial
 Creating NURBS Curves and Surfaces
Creating NURBS Curves and Surfaces![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
controlPoints1 = []
controlPoints1.append( IVec(0, 0, 0) )
controlPoints1.append( IVec(20, 30, 30) )
controlPoints1.append( IVec(40, -30, -30) )
controlPoints1.append( IVec(60, 0, 0) )
deg1 = 3
ICurve(controlPoints1, deg1).clr(0)
controlPoints2 = []
controlPoints2.append( IVec4(0, 0, 0, 1) )
controlPoints2.append( IVec4(20, 30, 30, 0.5) )
controlPoints2.append( IVec4(40, -30, -30, 0.5) )
controlPoints2.append( IVec4(60, 0, 0, 1) )
deg2 = 3
ICurve(controlPoints2, deg2).clr(1.,0,0)
controlPoints3 = [ \
[ IVec(-70,0,0), IVec(-70,20,30), IVec(-70,40,0) ], \
[ IVec(-50,30,30), IVec(-50,50,60), IVec(-50,70,30) ], \
[ IVec(-30,-30,-30), IVec(-30,-10,0), IVec(-30,10,-30) ], \
[ IVec(-10,0,30), IVec(-10,20,60), IVec(-10,40,30) ] ]
udeg3 = 3
vdeg3 = 2
ISurface(controlPoints3, udeg3, vdeg3).clr(0)
controlPoints4 = [ \
[ IVec4(-70,0,0,1), IVec4(-70,20,30,.5), IVec4(-70,40,0,1) ], \
[ IVec4(-50,30,30,.5), IVec4(-50,50,60,.5), IVec4(-50,70,30,.5) ], \
[ IVec4(-30,-30,-30,.5), IVec4(-30,-10,0,.5), IVec4(-30,10,-30,.5) ], \
[ IVec4(-10,0,30,1), IVec4(-10,20,60,.5), IVec4(-10,40,30,1) ] ]
udeg4 = 3
vdeg4 = 2
ISurface(controlPoints4, udeg4, vdeg4).clr(1,.5,1)

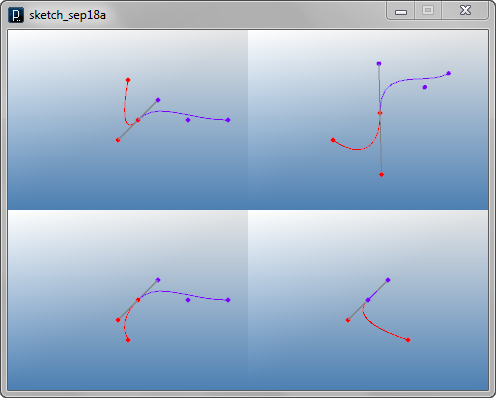
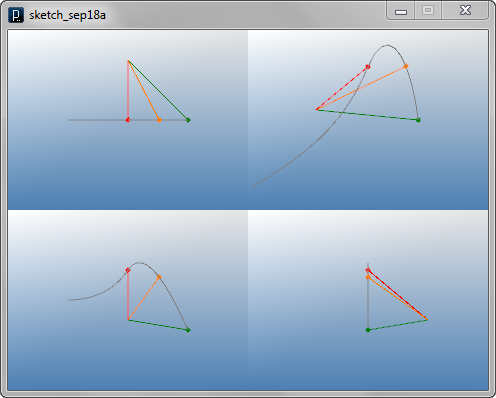
 Continuity of NURBS Geometry
Continuity of NURBS Geometry![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
curveEdgePt = IVec(10,0,0)
curveTangent = IVec(20,20,20)
cpts1 = []
cpts1.append( curveEdgePt )
cpts1.append( curveEdgePt.dup().sub(curveTangent) )
cpts1.append( IVec(0, 40, -40) )
cpts2 = []
cpts2.append( curveEdgePt )
cpts2.append( curveEdgePt.dup().add(curveTangent) )
cpts2.append( IVec(60,0,0) )
cpts2.append( IVec(100,0,0) )
ICurve(cpts1, 2).clr(1.,0,0)
ICurve(cpts2, 3).clr(.5,0,1)
# showing control points
for pt in cpts1 :
IPoint(pt).clr(1.,0,0)
for pt in cpts2 :
IPoint(pt).clr(.5,0,1)
# showing straight relationship
ICurve(cpts1[1], cpts2[1])
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
surfaceTangent1 = IVec(20, 0, -10)
surfaceTangent2 = IVec(20, -20, -10)
surfaceEdgePt1 = IVec(0, 0, 0)
surfaceEdgePt2 = IVec(0, 30, 0)
cpts3 = []
cpts3.append([])
cpts3[0].append(surfaceEdgePt1)
cpts3[0].append(surfaceEdgePt2)
cpts3.append([])
cpts3[1].append(surfaceEdgePt1.dup().sub(surfaceTangent1))
cpts3[1].append(surfaceEdgePt2.dup().sub(surfaceTangent2))
cpts3.append([])
cpts3[2].append(IVec(-10, 0, -30))
cpts3[2].append(IVec(-10, 30, -30))
cpts4 = []
cpts4.append([])
cpts4[0].append(surfaceEdgePt1)
cpts4[0].append(surfaceEdgePt2)
cpts4.append([])
cpts4[1].append(surfaceEdgePt1.dup().add(surfaceTangent1))
cpts4[1].append(surfaceEdgePt2.dup().add(surfaceTangent2))
cpts4.append([])
cpts4[2].append(IVec(10, 0, 30))
cpts4[2].append(IVec(10, 30, 30))
ISurface(cpts3, 2, 1).clr(0,0,1.)
ISurface(cpts4, 2, 1).clr(0,.5,1.)
# showing control points
for pts in cpts3 :
for pt in pts :
IPoint(pt).clr(0,0,1.)
for pts in cpts4 :
for pt in pts :
IPoint(pt).clr(0,.5,1.)
# showing straight relationship
ICurve(cpts3[1][0], cpts4[1][0])
ICurve(cpts3[1][1], cpts4[1][1])
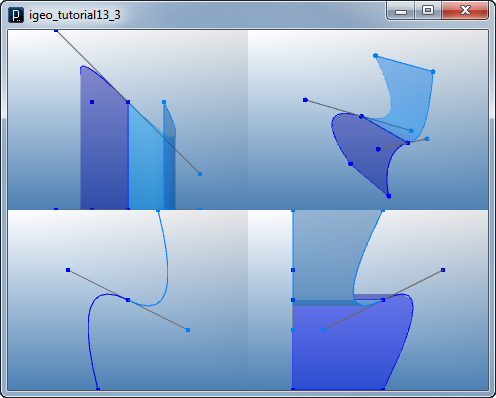
 Point on NURBS Curve
Point on NURBS Curve![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [ IVec(-60,0,0), IVec(-20,0,0), IVec(20,0,60), IVec(60,0,-30) ]
curve = ICurve(cpts, 2)
pt1 = curve.pt(0.5)
pt2 = curve.pt(0.8)
pt3 = curve.pt(1.0)
# showing points
IPoint(pt1).clr(1.,0,0)
IPoint(pt2).clr(1.,.5,0)
IPoint(pt3).clr(0,.5,0)
# using them for creating other geometries
ICurve(IVec(0,60,-20), pt1).clr(1.,0,0)
ICurve(IVec(0,60,-20), pt2).clr(1.,.5,0)
ICurve(IVec(0,60,-20), pt3).clr(0,.5,0)
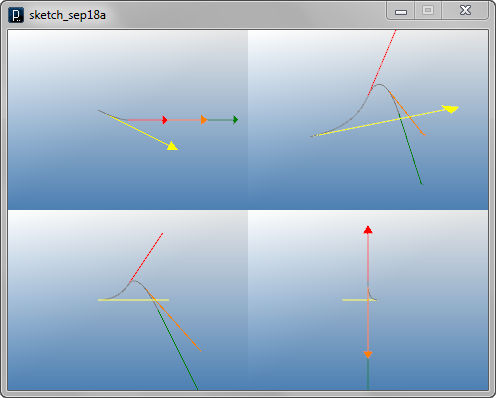
 Tangent on NURBS Curve
Tangent on NURBS Curve![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [ IVec(-30,10,0), IVec(-10,0,0), IVec(10,0,30), IVec(30,0,-10) ]
curve = ICurve(cpts, 2)
tan1 = curve.tan(0)
tan2 = curve.tan(0.5)
tan3 = curve.tan(0.8)
tan4 = curve.tan(1.0)
# showing arrows at each point on the curve
tan1.show(curve.pt(0)).clr(1.,1.,0).size(10)
tan2.show(curve.pt(0.5)).clr(1.,0,0).size(10)
tan3.show(curve.pt(0.8)).clr(1,.5,0).size(10)
tan4.show(curve.pt(1.0)).clr(0,.5,0).size(10)
 Point on NURBS Surface
Point on NURBS Surface![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [[ IVec(-40,-20,-20), IVec(0,0,0), IVec(40,0,-20) ], \
[ IVec(-40,30,20), IVec(0,30,0), IVec(40,30,-10) ]]
surface = ISurface(cpts,1,2)
pt1 = surface.pt(0.5,0.5)
pt2 = surface.pt(0.5,1.0)
pt3 = surface.pt(0.3,0.2)
# showing points
IPoint(pt1).clr(1.,0,0)
IPoint(pt2).clr(1,.5,0)
IPoint(pt3).clr(0,.5,0)
# using them for creating other geometries
ICurve(IVec(-20,0,40), pt1).clr(1.,0,0)
ICurve(IVec(-20,0,40), pt2).clr(1,.5,0)
ICurve(IVec(-20,0,40), pt3).clr(0,.5,0)
 Tangent on NURBS Surface
Tangent on NURBS Surface![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [[ IVec(-40,-20,-20), IVec(0,0,0), IVec(40,0,-20) ], \
[ IVec(-40,30,20), IVec(0,30,0), IVec(40,30,-10) ]]
surface = ISurface(cpts,1,2)
utan1 = surface.utan(0.5,0.5)
utan2 = surface.utan(0.5,1.0)
vtan1 = surface.vtan(0.5,0.5)
vtan2 = surface.vtan(0.5,1.0)
# showing arrows at each point on the surface
utan1.show(surface.pt(0.5,0.5)).clr(1.,0,0).size(5)
utan2.show(surface.pt(0.5,1.0)).clr(0,0,1.).size(5)
vtan1.show(surface.pt(0.5,0.5)).clr(1,.5,0).size(5)
vtan2.show(surface.pt(0.5,1.0)).clr(0,.5,1).size(5)
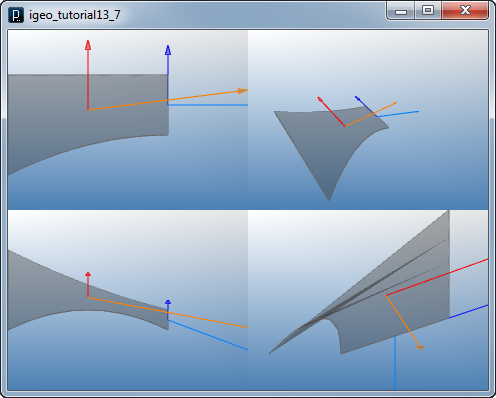
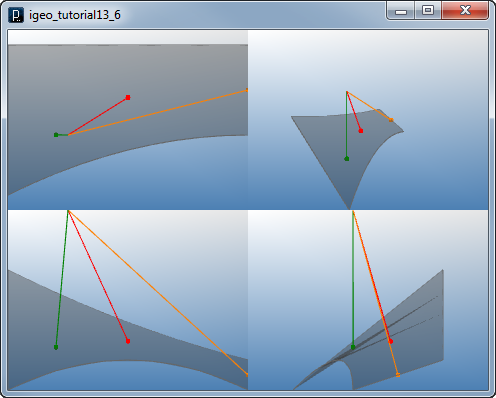
 Normal on NURBS Surface
Normal on NURBS Surface![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [[ IVec(-40,30,20), IVec(0,30,0), IVec(40,30,-10) ], \
[ IVec(-40,-20,-20), IVec(0,0,0), IVec(40,0,-20) ]]
surface = ISurface(cpts,1,2)
normal1 = surface.nml(0.5,0.5).len(40)
normal2 = surface.nml(1.0,0.5).len(40)
normal3 = surface.nml(0.0,0.5).len(40)
normal4 = surface.nml(0.2,0.8).len(40)
# showing arrows at each point on the surface
normal1.show(surface.pt(0.5,0.5)).clr(1.,0,0).size(10)
normal2.show(surface.pt(1.0,0.5)).clr(1.,.5,0).size(10)
normal3.show(surface.pt(0.0,0.5)).clr(0,.5,0).size(10)
normal4.show(surface.pt(0.2,0.8)).clr(0,.5,1).size(10)
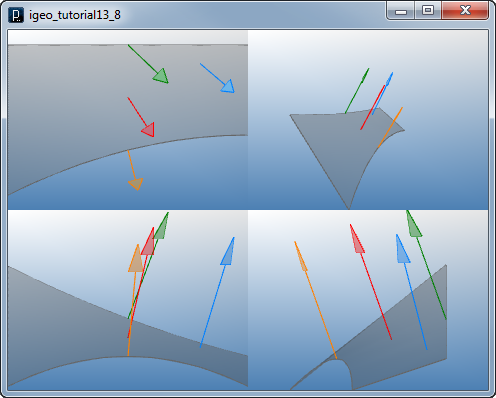
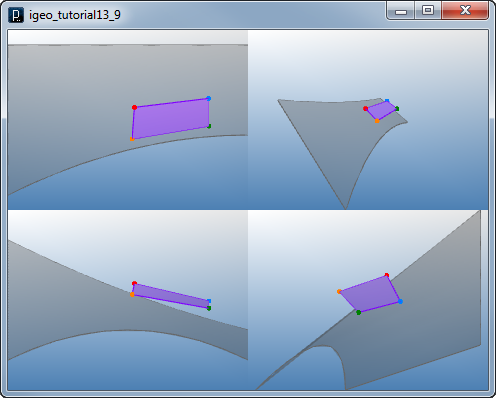
 Offset Point on NURBS Surface
Offset Point on NURBS Surface![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
cpts = [[ IVec(-40,30,20), IVec(0,30,0), IVec(40,30,-10) ], \
[ IVec(-40,-20,-20), IVec(0,0,0), IVec(40,0,-20) ]]
surface = ISurface(cpts,1,2)
pt1 = surface.pt(0.5, 0.5, 10)
pt2 = surface.pt(0.8, 0.5, 10)
pt3 = surface.pt(0.8, 0.8, 10)
pt4 = surface.pt(0.5, 0.8, 10)
# showing points
IPoint(pt1).clr(1.,0,0)
IPoint(pt2).clr(1.,.5,0)
IPoint(pt3).clr(0,.5,0)
IPoint(pt4).clr(0,.5,1)
# using them for creating other geometries
ISurface(pt1,pt2,pt3,pt4).clr(.5,0,1)
 HOME
HOME
 FOR PROCESSING
FOR PROCESSING
 DOWNLOAD
DOWNLOAD
 DOCUMENTS
DOCUMENTS
 TUTORIALS (Java /
Python)
TUTORIALS (Java /
Python)
 GALLERY
GALLERY
 SOURCE CODE(GitHub)
SOURCE CODE(GitHub)
 PRIVACY POLICY
PRIVACY POLICY
 ABOUT/CONTACT
ABOUT/CONTACT
