
 Python Tutorials Python Tutorials | (back to the list of tutorials) |
 For Loop
For Loop
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
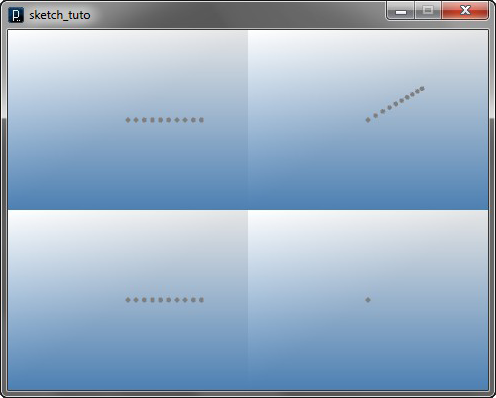
for i in range(10):
IPoint(i, 0, 0)
The code above is equivalent to this code.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
IPoint(0,0,0) # 1st execution. i=0
IPoint(1,0,0) # 2nd execution. i=1
IPoint(2,0,0) # 3rd execution. i=2
IPoint(3,0,0) # 4th execution. i=3
IPoint(4,0,0) # 5th execution. i=4
IPoint(5,0,0) # 6th execution. i=5
IPoint(6,0,0) # 7th execution. i=6
IPoint(7,0,0) # 8th execution. i=7
IPoint(8,0,0) # 9th execution. i=8
IPoint(9,0,0) #10th execution. i=9
Please note that the last point is at (9, 0, 0), not (10, 0, 0) but total number of points is still ten because it started with zero.
 This diagram on the right shows the flow of the execution.
This diagram on the right shows the flow of the execution.
 Logics inside Body
Logics inside BodyThe example code above just shows the repetition of ten times. Formation of geometries created in a repetition is up to the way you use the counting number i to create geometries. This is a fundamental part of design of an algorithm.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
for i in range(10):
IPoint(0, 0, i*5)
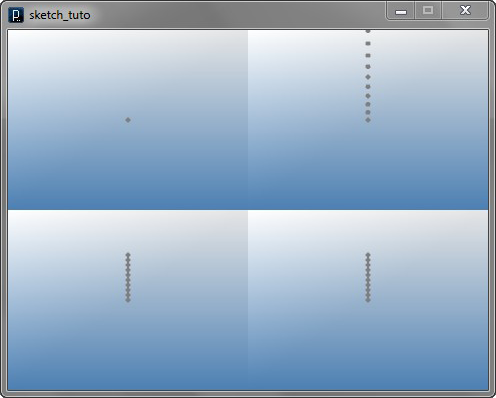
Instead of shifting points in X direction, this code shifts points in Z direction in the increment of 5.
This code below sets the color of points according to the counting number i.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
for i in range(10):
IPoint(0, 0, i*5).clr(i*0.1,0,0)

Another example code of putting the counter i into parameters of geometries.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
for i in range(10):
IPoint(i*10-50, 10-i*5, i*4).clr(i*0.1, 1.0-i*0.1, 0)

To understand the behavior of those parameters, let's see the equivalent unrolled code below.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
IPoint(-50, 10, 0).clr( 0, 1.0, 0) # i=0
IPoint(-40, 5, 4).clr(0.1, 0.9, 0) # i=1
IPoint(-30, 0, 8).clr(0.2, 0.8, 0) # i=2
IPoint(-20, -5, 12).clr(0.3, 0.7, 0) # i=3
IPoint(-10, -10, 16).clr(0.4, 0.6, 0) # i=4
IPoint( 0, -15, 20).clr(0.5, 0.5, 0) # i=5
IPoint( 10, -20, 24).clr(0.6, 0.4, 0) # i=6
IPoint( 20, -25, 28).clr(0.7, 0.3, 0) # i=7
IPoint( 30, -30, 32).clr(0.8, 0.2, 0) # i=8
IPoint( 40, -35, 36).clr(0.9, 0.1, 0) # i=9
Yet another example code of putting the counter i into parameters of geometries using trigonometric functions.
![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
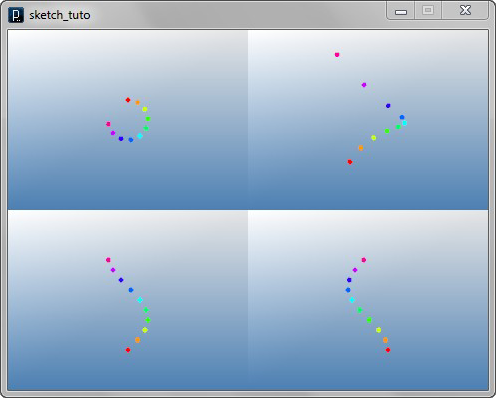
for i in range(10):
IPoint(sin(i*0.5)*20, \
cos(i*0.5)*20, \
i*10-50).hsb(i*0.1,1,1)
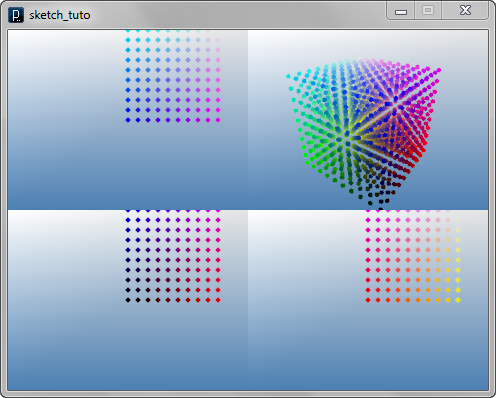
 Nested Loop (2 Dimensional For Loop)
Nested Loop (2 Dimensional For Loop)![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
for i in range(10):
for j in range(10):
IPoint(i*10, j*10, 0).clr(i*0.1, j*0.1, 0)

 Nested Loop (3 Dimensional For Loop)
Nested Loop (3 Dimensional For Loop)![]()
![]()
![]()
![]()
add_library('igeo')
size( 480, 360, IG.GL )
for i in range(10):
for j in range(10):
for k in range(10):
IPoint(i*10, j*10, k*10).clr(i*0.1, j*0.1, k*0.1)
 HOME
HOME
 FOR PROCESSING
FOR PROCESSING
 DOWNLOAD
DOWNLOAD
 DOCUMENTS
DOCUMENTS
 TUTORIALS (Java /
Python)
TUTORIALS (Java /
Python)
 GALLERY
GALLERY
 SOURCE CODE(GitHub)
SOURCE CODE(GitHub)
 PRIVACY POLICY
PRIVACY POLICY
 ABOUT/CONTACT
ABOUT/CONTACT
