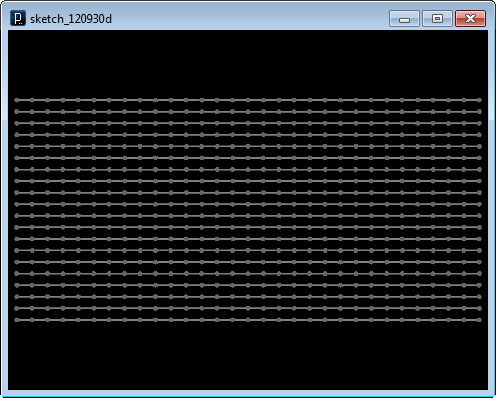
最初のコードでは、入力ファイルから読み込まれた直線を等分割して、直線上に複数のパーティクル・エージェントを 配置し、その間を張力線でつないでいます。 用いた入力ファイルは以下です。
tension_lines1.3dm.

import processing.opengl.*;
import igeo.*;

size(480, 360, IG.GL);
IG.bg(0);
IG.open("tension_lines1.3dm");
ICurve[] curves = IG.curves();

int division=30;
double inc = 1.0/division;

for (int i=0; i < curves.length; i++) {
  IParticle[] pts = new IParticle[division+1];
  for (int j=0; j <= division; j++) { // creating particles
    pts[j] = new IParticle( curves[i].pt( j*inc ) ).fric(0.01);
  }
  pts[0].fix(); // fixing the start point
  pts[division].fix(); // fixing the end point
  for (int j=0; j < division; j++) { // connecting particles
    new ITensionLine(pts[j], pts[j+1]).tension(150).clr(1.0, 0.5).weight(2);
  }
  curves[i].del();
}

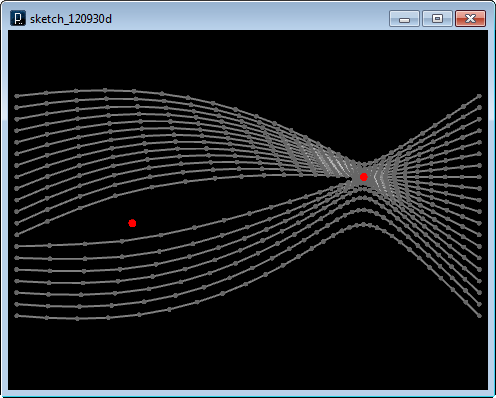
上のコードでは外部の力の場はなにもありませんが、 次に、斥力アトラクタ―を二つ配置して、 線がどのように変形されるかを見ます。

import processing.opengl.*;
import igeo.*;

size(480, 360, IG.GL);
IG.bg(0);
IG.open("tension_lines1.3dm");
ICurve[] curves = IG.curves();

new IAttractor(15, 6, 0).intensity(10).linear(30).clr(1.0,0,0).size(8);
new IAttractor(5, 4, 0).intensity(-30).linear(10).clr(1.0,0,0).size(8);

int division=30;
double inc = 1.0/division;

for (int i=0; i < curves.length; i++) {
  IParticle[] pts = new IParticle[division+1];
  for (int j=0; j <= division; j++) { // creating particles
    pts[j] = new IParticle( curves[i].pt( j*inc ) ).fric(0.01);
  }
  pts[0].fix(); // fixing the start point
  pts[division].fix(); // fixing the end point
  for (int j=0; j < division; j++) { // connecting particles
    new ITensionLine(pts[j], pts[j+1]).tension(150).clr(1.0, 0.5).weight(2);
  }
  curves[i].del();
}

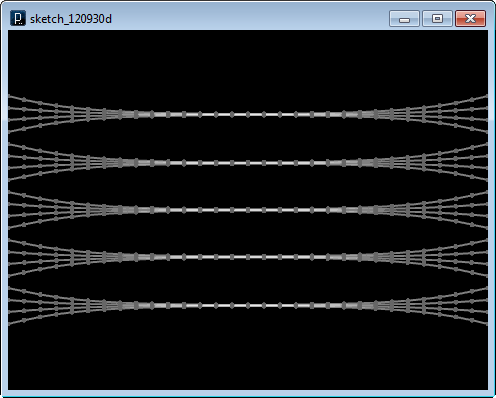
三つ目のコードでは、パーティクル・エージェントの代わりにスウォーム・エージェントを直線上に配置しています。 スウォーム・アルゴリズムの結束規則により、線は集結しようとしますが、張力によって引き戻されます。

import processing.opengl.*;
import igeo.*;

size(480, 360, IG.GL);
IG.bg(0);
IG.open("tension_lines1.3dm");
ICurve[] curves = IG.curves();

int division=30;
double inc = 1.0/division;

for (int i=0; i < curves.length; i++) {
  IBoid[] pts = new IBoid[division+1];
  for (int j=0; j <= division; j++) { // creating particles
    pts[j] = new IBoid( curves[i].pt( j*inc ) ).fric(0.1);
    pts[j].cohesionDist(1);
    pts[j].cohesionRatio(10);
    pts[j].separationRatio(0);
    pts[j].alignmentRatio(0);
  }
  pts[0].fix(); // fixing the start point
  pts[division].fix(); // fixing the end point
  for (int j=0; j < division; j++) { // connecting particles
    new ITensionLine(pts[j], pts[j+1]).tension(150).clr(1.0, 0.5).weight(2);
  }
  curves[i].del();
}

次の例では、コードはほぼ一緒ですが、入力ファイルの直線データだけを変更しています。 以前の例の並行線ではなく、交差する直線を用いると、 交差する周辺で束になろうとする状況が良く観察できます。 この例で用いた入力ファイルは以下です。
tension_lines2.3dm

import processing.opengl.*;
import igeo.*;

size(480, 360, IG.GL);
IG.bg(0);
IG.open("tension_lines2.3dm");
ICurve[] curves = IG.curves();

int division=50;
double inc = 1.0/division;

for (int i=0; i < curves.length; i++) {
  IBoid[] pts = new IBoid[division+1];
  for (int j=0; j <= division; j++) { // creating particles
    pts[j] = new IBoid( curves[i].pt( j*inc ) ).fric(0.1);
    pts[j].cohesionDist(0.5);
    pts[j].cohesionRatio(50);
    pts[j].separationRatio(0);
    pts[j].alignmentRatio(0);
    pts[j].hide();
  }
  pts[0].fix(); // fixing the start point
  pts[division].fix(); // fixing the end point
  for (int j=0; j < division; j++) { // connecting particles
    new ITensionLine(pts[j], pts[j+1]).tension(100).clr(1.0, 0.5).weight(2);
  }
  curves[i].del();
}

シミュレーションが始まる前の初期状態ではランダムに交差する直線に見えます。

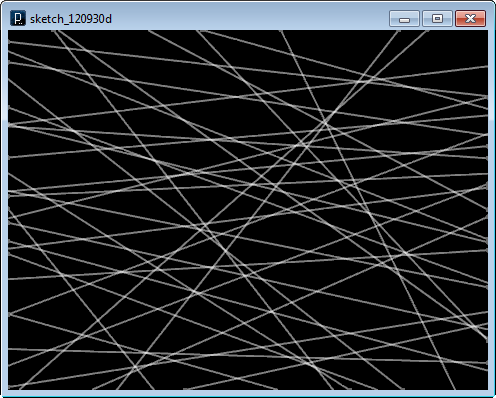
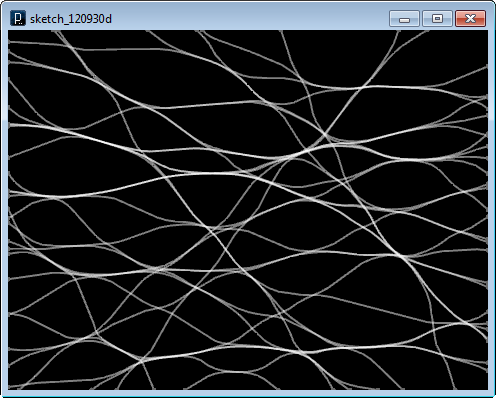
十分に時間がたつと力の関係が平衡の状態になります。