
 チュートリアル チュートリアル | (トピック一覧へ戻る) |
 配列による曲線の生成
配列による曲線の生成
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size( 480, 360, IG.GL );
IVec[] cpts1 = new IVec[4];
cpts1[0] = new IVec(-30, 10, 0);
cpts1[1] = new IVec(-10, 10, 0);
cpts1[2] = new IVec(-10, 30, 0);
cpts1[3] = new IVec(-30, 30, 0);
// curve 1 (red)
new ICurve(cpts1, 3).clr(1.,0,0);
IVec[] cpts2 = new IVec[10];
for(int i=0; i < cpts2.length; i++){
if(i%2==0){ cpts2[i] = new IVec(i*10, 0, 0); }
else{ cpts2[i] = new IVec(i*10, 10, 0); }
}
// curve 2 (blue)
new ICurve(cpts2, 1).clr(0,0,1.);
IVec[] cpts3 = new IVec[16];
for(int i=0; i < cpts3.length; i++){
if(i%4==0){ cpts3[i] = new IVec(-30, -10, i*5); }
else if(i%4==1){ cpts3[i] = new IVec(-10, -10, i*5); }
else if(i%4==2){ cpts3[i] = new IVec(-10, -30, i*5); }
else{ cpts3[i] = new IVec(-30, -30, i*5); } // same with i%4==3
}
// curve 3 (cyan)
new ICurve(cpts3, 3).clr(0,1.,1.);
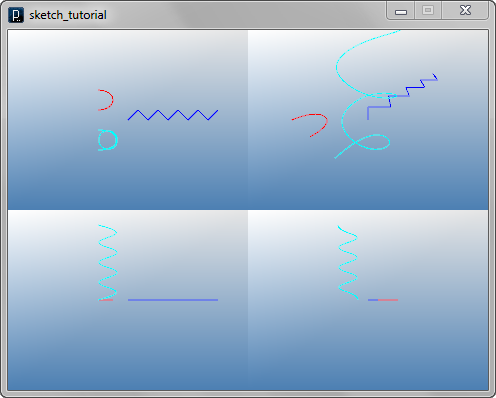
 配列による曲面の生成
配列による曲面の生成
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size( 480, 360, IG.GL );
IVec[][] cpts1 = new IVec[2][2];
cpts1[0][0] = new IVec( 0, 0, 0);
cpts1[1][0] = new IVec(-30, 0, 0);
cpts1[0][1] = new IVec( 0,-30, 0);
cpts1[1][1] = new IVec(-30,-30, 0);
// surface 1 (gray)
new ISurface(cpts1);
IVec[][] cpts2 = new IVec[10][2];
for(int i=0; i < cpts2.length; i++){
if(i%2==0){
cpts2[i][0] = new IVec(i*10,0,0);
cpts2[i][1] = new IVec(i*10,0,20);
}
else{
cpts2[i][0] = new IVec(i*10,-10,0);
cpts2[i][1] = new IVec(i*10,10,10);
}
}
// surface 2 (purple)
new ISurface(cpts2).clr(.5,0,1);
IVec[][] cpts3 = new IVec[4][4];
for(int i=0; i < cpts3.length; i++){
for(int j=0; j < cpts3[i].length; j++){
if( (i==0||i==3) && (j==1||j==2) ){
cpts3[i][j] = new IVec(-i*10, j*10, 20);
}
else{ cpts3[i][j] = new IVec(-i*10, j*10, 0); }
}
}
// surface 3 (pink)
new ISurface(cpts3,3,3).clr(1,.5,1);
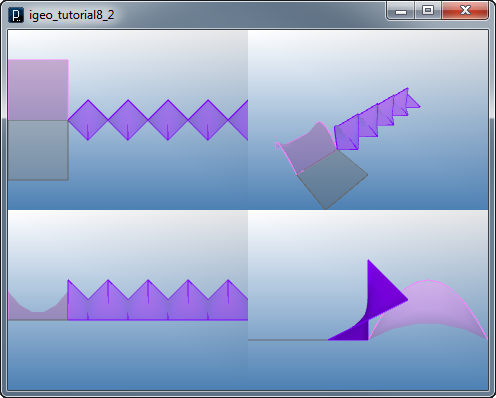
 配列によるポリゴン・メッシュの生成
配列によるポリゴン・メッシュの生成
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size( 480, 360, IG.GL );
IVec[][] cpts1 = new IVec[10][10];
for(int i=0; i < cpts1.length; i++){
for(int j=0; j < cpts1[i].length; j++){
if( (i+j)%2==0 ){
cpts1[i][j] = new IVec(i*5, -j*5-30, (i+j)*2);
}
else{ cpts1[i][j] = new IVec(i*5, -j*5-30, (i+j-1)*2); }
}
}
// mesh 1 (cyan)
new IMesh(cpts1).clr(0,1.,1.);
int divNum=30;
IVec[][] cpts2 = new IVec[10][divNum+1];
for(int i=0; i < cpts2.length; i++){
for(int j=0; j < cpts2[i].length; j++){
float radius = 30 - i*3;
float angle = 2 * PI / divNum * j;
cpts2[i][j] =
new IVec(cos(angle)*radius, sin(angle)*radius, i*i*.5);
}
}
// mesh 2 (red)
new IMesh(cpts2).clr(1.,0,0);
円周率を表す定数PIが三角法関数の生成に利用されていることに注目してください。
sin()とcos()は角度ではなくラジアンであるため、
divNumは360ではなく2 * PIを割ります。
またcpts2の内側の配列長がdivNumに1を加算していることにも注意してください。
筒形状の最初の辺と最後の辺を連結するため、面が余計に必要となっています。
 HOME
HOME
 FOR PROCESSING
FOR PROCESSING
 DOWNLOAD
DOWNLOAD
 DOCUMENTS
DOCUMENTS
 TUTORIALS (Java /
Python)
TUTORIALS (Java /
Python)
 GALLERY
GALLERY
 SOURCE CODE(GitHub)
SOURCE CODE(GitHub)
 PRIVACY POLICY
PRIVACY POLICY
 ABOUT/CONTACT
ABOUT/CONTACT
