
 チュートリアル チュートリアル | (トピック一覧へ戻る) |
 重力とアトラクタ―
重力とアトラクタ―
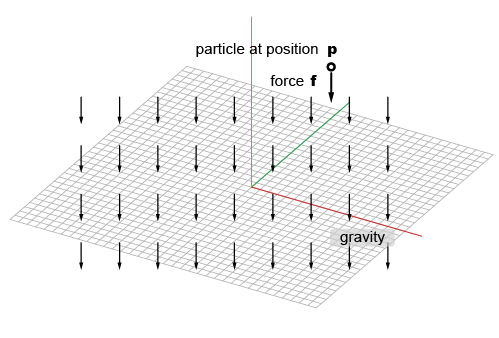
アトラクタ―と斥力はある一点からの差ベクトルによって力が定義されます。

以前のチュートリアルでは重力やアトラクタ―はユーザーのクラスとして定義されていましたが、
iGeoではライブラリにIGravityクラスやIAttractorクラスが
用意されており、クラスを定義せずともそれらの力を用いることができます。
以下の例では、IGravityクラスの利用例が示されます。
重力のベクトル方向のX,Y,Zをコンストラクタに指定することで重力が定義されます。
このコードでは、IParticleクラスの代わりに
IParticleTrajectoryクラスが用いられています。
このパーティクル・エージェントは、軌跡を線として生成しながら移動します。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.duration(50);
new IGravity(0,0,-10); // direction and intensity of gravity
for(int i=0; i < 100; i++){
new IParticleTrajectory(IRand.pt(-100,100));// random points from (-100,-100,-100) to (100,100,100)
}
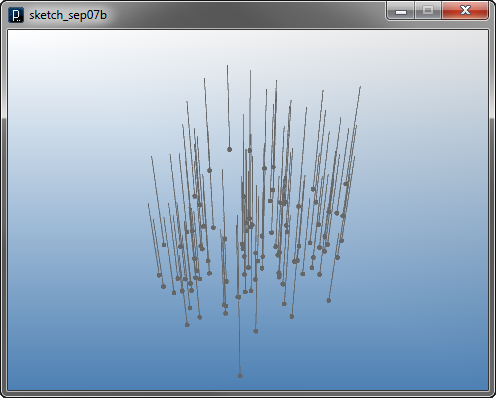
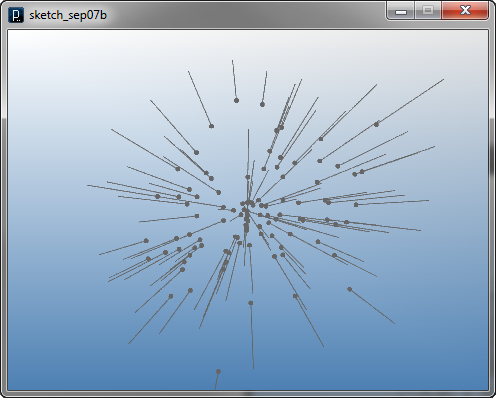
下のコードでは、IAttractorクラスの利用例が示されます。 コンストラクタにアトラクタ―の位置を指定し、力の強さは intensity(double)メソッドによって指定します。 これに設定する値が正であれば、中心に向かって引っ張るアトラクターとなり、 負であれば、斥力となります。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.duration(100);
new IAttractor(0,0,0).intensity(10); // attractor at (0,0,0) with intensity 10
for(int i=0; i < 100; i++){
new IParticleTrajectory(IRand.pt(-100,100));// random points from (-100,-100,-100) to (100,100,100)
}
 力の場の可視化
力の場の可視化
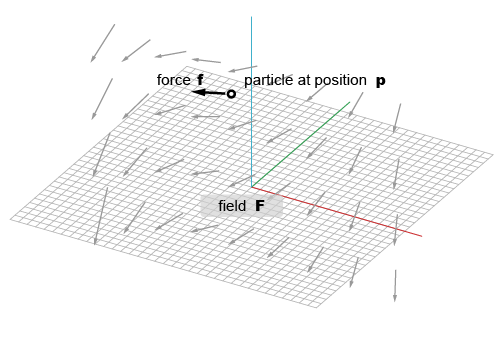
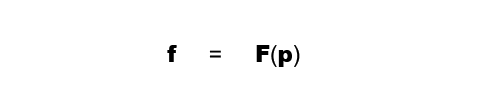
位置が変われば力のベクトルも変わるため、
力の場を理解するためには、多くの位置でのベクトルを見てみる必要があります。
iGeoライブラリではIFieldVisualizerクラスを用いると、
ある空間の範囲内の指定された数の場所で力の場を調べて、
矢印として表示します。
以下のコードのように、最小と最大のX,Y,Z値の6つの値を与えて生成すると、
その範囲内でデフォルトの10×10×10の1000個の矢印が表示されます。
![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(-50,0,0).intensity(10).clr(1.0,0,0);//attractor new IAttractor(50,0,0).intensity(-10).clr(0,0,1.0);//repulsion // creating 3D matrix. default is 10x10x10. // input argument is (minX, minY, minZ, maxX, maxY, maxZ) new IFieldVisualizer(-100,-100,-100,100,100,100);
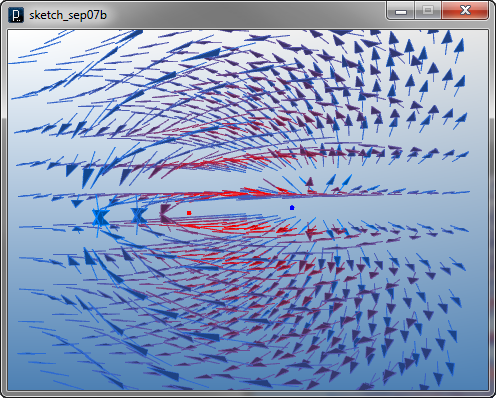
入力としてさらに3つの整数をX,Y,Zのサンプル数として与えると、その数で空間を分割して 力の場のベクトルをサンプルします。 また、Zのサンプル数を1とすると、2次元のベクトル場表示となります。
![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(-50,0,0).intensity(10).clr(1.0,0,0);//attractor new IAttractor(50,0,0).intensity(-10).clr(0,0,1.0);//repulsion // last 3 inputs are sample number in x, y, z. new IFieldVisualizer(-100, -50, 0, 100, 50, 0, 40, 20, 1);
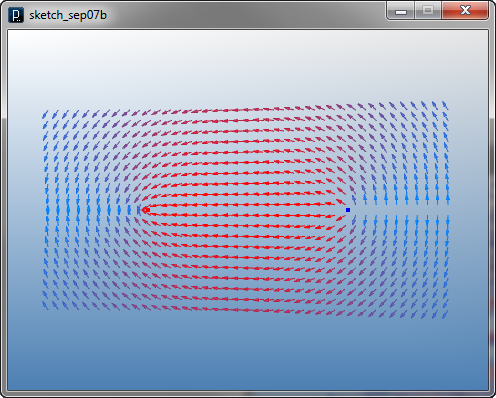
力の大きさは、色で表示されています。 この色は colorRange(min red, min green, min blue, max red, max green, max blue)メソッド で設定することができます。 また、力の大きさを矢印の長さでも表示したい場合は、 fixLength(boolean)メソッドにfalseを設定することによってできます。
![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(-50,0,0).intensity(10).clr(1.0,0,0);//attractor new IAttractor(50,0,0).intensity(-10).clr(0,0,1.0);//repulsion IFieldVisualizer visualizer = new IFieldVisualizer(-100, -50, 0, 100, 50, 0, 40, 20, 1); // color of min/max intensty. inputs are (min red, green, blue, max red, green, blue) visualizer.colorRange(0.0,0.0,0.0, 0.0,1.0,0.); // use variable length; now length is proportioanl to the intensity visualizer.fixLength(false);

 力の場の減衰
力の場の減衰減衰が無い場合は、距離によって力の強さが減衰せずに一定となります。 iGeoの力の場のクラスのほとんどはこれがデフォルトの設定となっており、 距離が遠くとも力が及ぼされるようになっています。 明示的にこの減衰設定するにはnoDecay()メソッドを実行します。

![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(0,0,0).noDecay(); new IFieldVisualizer(-100,-100,0,100,100,0,20,20,1).fixLength(false);

線形減衰は、以下のグラフのようにある距離へ直線的に減衰し、 指定された距離で力の大きさがゼロになります。 この減衰設定はlinearDecay(threshold)メソッドによりなされます。 メソッドの引数に、ゼロとなる距離を与えます。 このメソッドには短い別名メソッドlinear(threshold)もあります。

![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(0,0,0).linearDecay(100); new IFieldVisualizer(-100,-100,0,100,100,0,20,20,1).fixLength(false);

ガウス減衰は、以下のグラフのようにガウス関数をもちいたなだらかな減衰で、 距離が遠くなっても完全にゼロになることはありませんが、限りなくゼロに近づいていきます。 この減衰設定はgaussianDecay(threshold)メソッドで設定できます。 引数に与える距離は、グラフに記された標準偏差の2倍の位置を指定します。 このメソッドには短い別名メソッドgaussian(threshold)と gauss(threshold)もあります。

![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IAttractor(0,0,0).gaussianDecay(100); new IFieldVisualizer(-100,-100,0,100,100,0,20,20,1).fixLength(false);
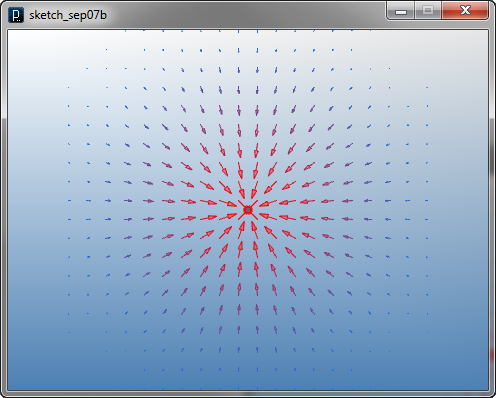
 点による力の場の定義
点による力の場の定義![]()
![]()
![]()
![]()
import processing.opengl.*; import igeo.*; size(480, 360, IG.GL); new IPointCurlField(new IVec(0,0,0), new IVec(0,0,1)).gaussianDecay(100); new IFieldVisualizer(-100,-100,0,100,100,0,20,20,1).fixLength(false);
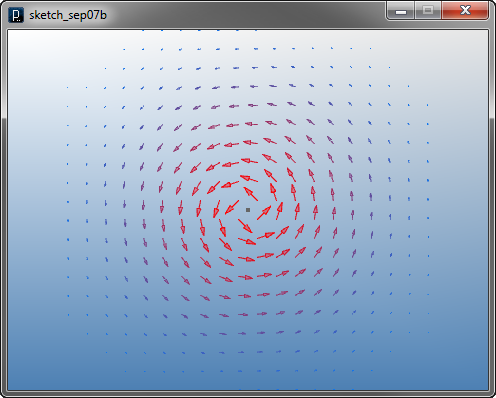
 曲線による力の場の定義
曲線による力の場の定義
まず曲線アトラクタ―は、パーティクルから最も近い曲線上の点にパーティクルを引き付けます。
この場はICurveAttractorFieldクラスによって生成できます。
入力として、以下のファイルのような曲線を与えます。この力の場を可視化したものも以下に示します。
curve_field1.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveAttractorField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
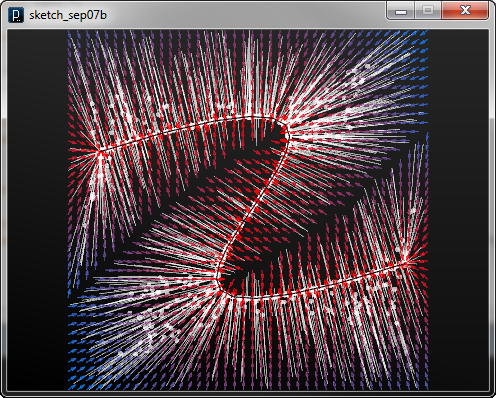
以下のコードでは、ランダムな位置に置かれたパーティクルが 曲線アトラクタ―に反応する様子が表示されます。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveAttractorField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}
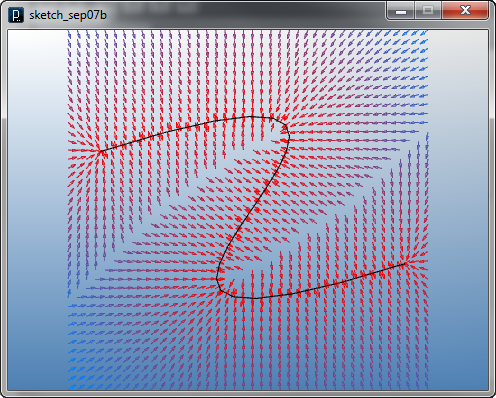
曲線流動場は、パーティクルから最寄りの曲線上の位置における 接線ベクトルを力として与えることによって定義されます。 曲線を入力としてICurveTangentFieldクラスを用いることで 生成できます。 以下のコードで力の場が可視化されます。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);

以下のコードでパーティクルの反応が見えます。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

3つめの曲線による力の場は曲線回転場です。 パーティクルには曲線の接線を軸として回転する力が与えられます。 ICurveCurlFieldに曲線を与えることによって 生成することができます。以下が可視化のコードです。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveCurlField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,-1, 20,20,1, 40,40,2);

以下がパーティクルの反応のコードです。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field1.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveCurlField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,-1, 20,20,1, 40,40,2);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}
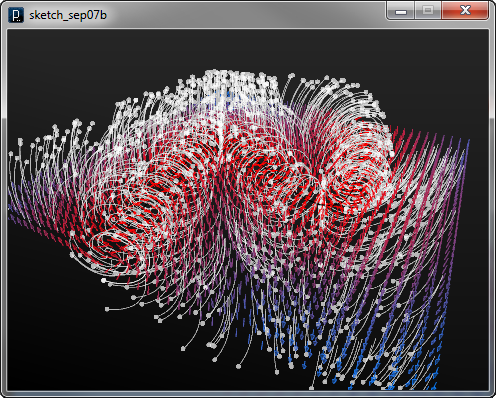
 力の場の重ね合わせ
力の場の重ね合わせ
例で用いられる2つの曲線は以下のファイルに含まれます。
curve_field2.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field2.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field2.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).intensity(10).linear(50);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

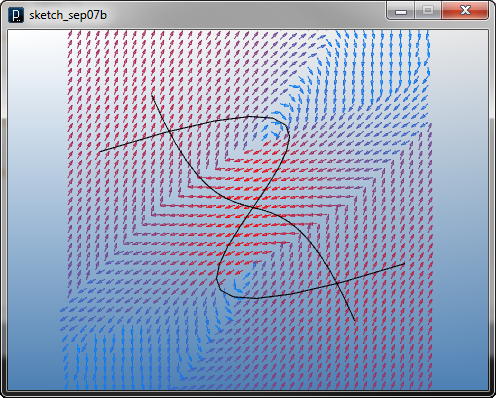
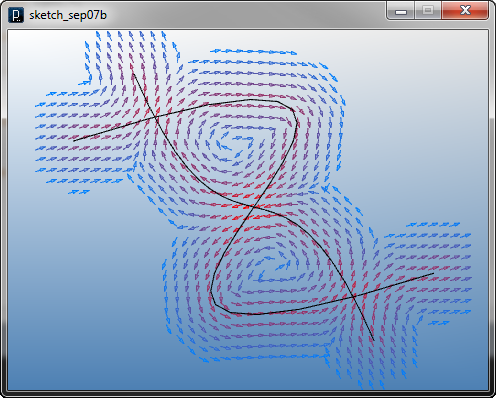
ベクトル和による単純な重ね合わせでは、特に力の場に減衰が無い場合、 ベクトルの方向が大きく変わったり、または打ち消されて力がゼロになったり、 パーティクルの反応が各々の力の場への反応から大きく異なることがあります。 以下に減衰を設定して遠くの位置では別の力の場からの影響が少なくなる場合を 示します。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field2.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).linear(5).intensity(10);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field2.3dm");
for(int i=0; i < IG.curveNum(); i++){
new ICurveTangentField(IG.curve(i)).linear(5).intensity(10);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

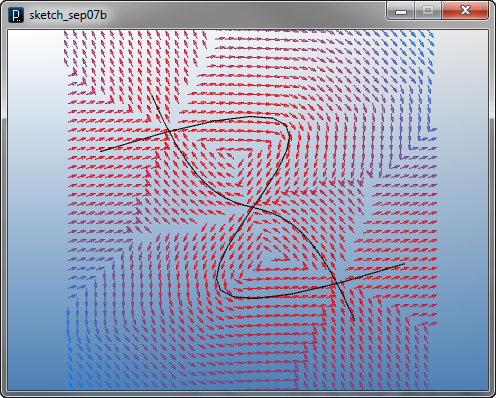
 距離に応じた力の場の複合
距離に応じた力の場の複合![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("curve_field2.3dm");
ICompoundField field = new ICompoundField();
for(int i=0; i < IG.curveNum(); i++){
field.add(new ICurveTangentField(IG.curve(i)).linear(50).intensity(10));
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field2.3dm");
ICompoundField field = new ICompoundField();
for(int i=0; i < IG.curveNum(); i++){
field.add(new ICurveTangentField(IG.curve(i)).linear(50).intensity(10));
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}
通常重力には起点となる場所がありませんが、
ICompoundFieldを用いるためには起点となる場所が必要になります。
そのために、IGravityクラスには起点をしていするコンストラクタ
以下のコードでは、様々な位置を起点として様々な方向に向けたIGravityを ICompoundFieldで複合させた結果を示します。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
ICompoundField field = new ICompoundField();
for(int i=0; i < 30; i++){
IVec dir = IRand.pt(-1,-1,1,1);
IVec pos = IRand.pt(-20,-20,20,20);
field.add(new IGravity(pos, dir));
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);

![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
ICompoundField field = new ICompoundField();
for(int i=0; i < 30; i++){
IVec dir = IRand.pt(-1,-1,1,1);
IVec pos = IRand.pt(-20,-20,20,20);
field.add(new IGravity(pos, dir));
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 2000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}
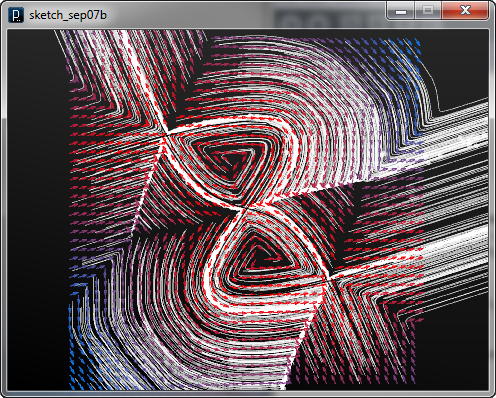
次の例では複数のIPointCurlFieldを ICompoundFieldで複合させた結果を示します。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
ICompoundField field = new ICompoundField();
for(int i=0; i < 30; i++){
field.add(new IPointCurlField(IRand.pt(-20,-20,20,20), new IVec(0,0,1)).gaussian(10));
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 2000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

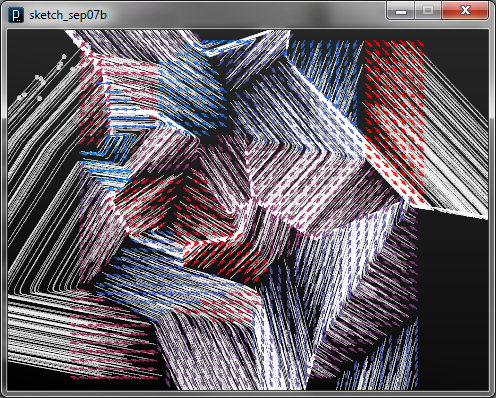
また、以下の例では IGravity、IAttractor、IPointCurlFieldを ICompoundFieldで複合させた結果を示します。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
ICompoundField field = new ICompoundField();
for(int i=0; i < 30; i++){
if(IRand.pct(40)){
field.add(new IAttractor(IRand.pt(-20,-20,20,20)).intensity(-10).gaussian(20));
}
else if(IRand.pct(50)){
field.add(new IPointCurlField(IRand.pt(-20,-20,20,20), new IVec(0,0,1)));
}
else{
field.add(new IGravity(IRand.pt(-20,-20,20,20),IRand.pt(-1,-1,1,1)));
}
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 2000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

 曲面による力の場の定義
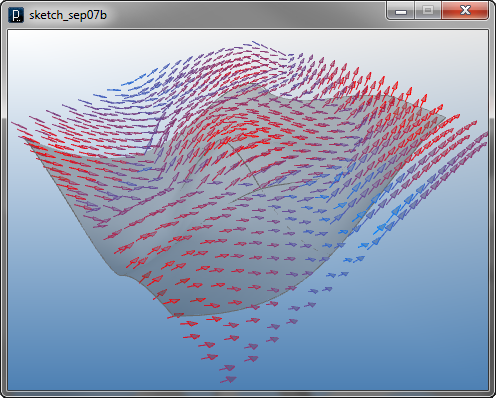
曲面による力の場の定義以下のコードではU方向への曲面流動場を ISurfaceUTangentFieldクラスによって生成します。 力の場は曲面のU方向の接線ベクトルによって定義されます。
例で用いられる曲面のファイルは以下です。
surface_field1.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new ISurfaceUTangentField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,-2, 20,20,0, 20,20,2);
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new ISurfaceUTangentField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,-2, 20,20,0, 20,20,2);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,-5,20,20,0)).fric(0.1).clr(1.0,0.7);
}
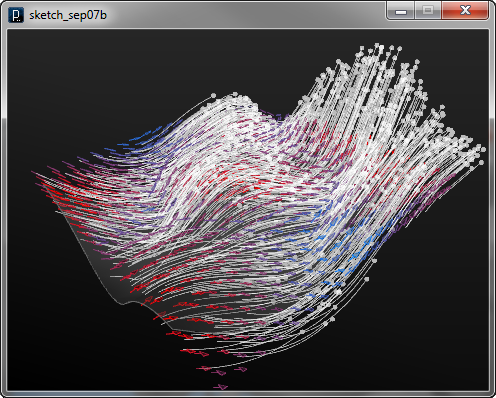
V方向への曲面流動場は ISurfaceVTangentFieldクラスによって生成されます。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new ISurfaceVTangentField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,-2, 20,20,0, 20,20,2);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,-5,20,20,0)).fric(0.1).clr(1.0,0.7);
}
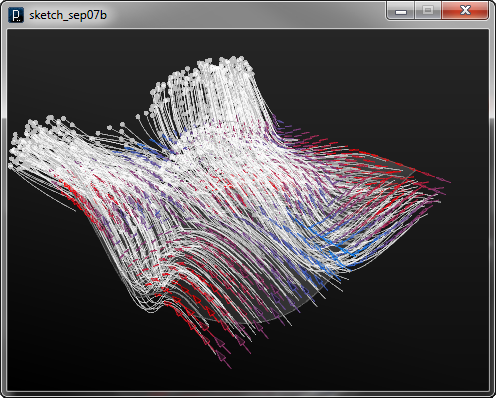
曲面法線場は曲面の法線ベクトルによって定義されます。 以下のコードでは ISurfaceNormalFieldクラスを用いて 生成しています。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new ISurfaceNormalField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,-2, 20,20,0, 20,20,2);
for(int i=0; i < 1000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,-5,20,20,0)).fric(0.1).clr(1.0,0.7);
}

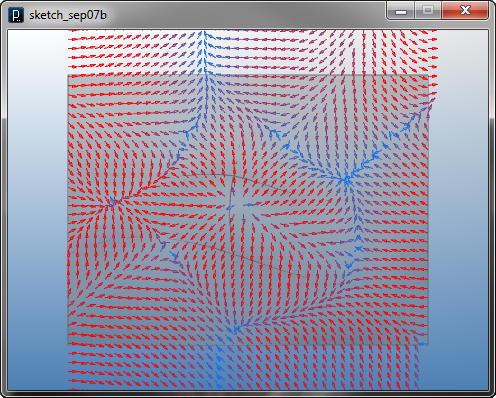
曲面勾配場は、曲面をZ方向を上とした丘のように見た時の勾配に応じて、 転げ落ちるような力を生成します。ただし、ここでは発生する力はXY方向のみで、 Z方向には発生しません。 この力の場はI2DSurfaceSlopeFieldクラスによって 生成できます。
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new I2DSurfaceSlopeField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("surface_field1.3dm");
for(int i=0; i < IG.surfaceNum(); i++){
new I2DSurfaceSlopeField(IG.surface(i)).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
for(int i=0; i < 2000; i++){
new IParticleTrajectory(IRand.pt(-20,-20,20,20)).fric(0.1).clr(1.0,0.7);
}

 入力ファイルの点からのパーティクルの生成
入力ファイルの点からのパーティクルの生成![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field_init1.3dm");
ICurve[] fieldCurves = IG.layer("field").curves();
for(int i=0; i < fieldCurves.length; i++){
new ICurveTangentField(fieldCurves[i]).linear(20).intensity(50);
}
IPoint[] points = IG.layer("particle").points();
for(int i=0; i < points.length; i++){
new IParticleTrajectory(points[i]).fric(0.2).clr(points[i].clr());
points[i].del();
}
以下に点の初期位置と、その力の場による移動結果が示されます。

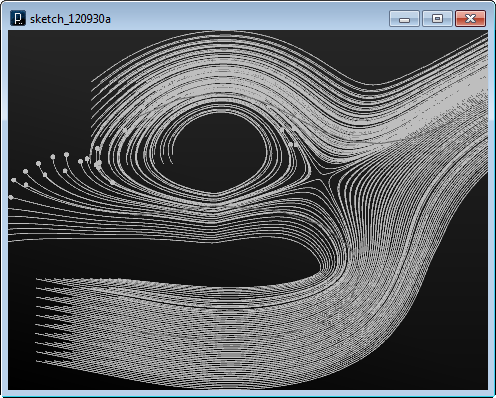
 入力ファイルの曲線からのパーティクルの生成
入力ファイルの曲線からのパーティクルの生成
例に用いられた入力ファイルは上のものと同様に、それぞれの曲線がレイヤー分けされています。
curve_field_init2.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.open("curve_field_init2.3dm");
ICurve[] fieldCurves = IG.layer("field").curves();
for(int i=0; i < fieldCurves.length; i++){
new ICurveTangentField(fieldCurves[i]).linear(20).intensity(50);
}
int divisionNum = 50;
ICurve[] particleCurves = IG.layer("particle").curves();
for(int i=0; i < particleCurves.length; i++){
for(int j=0; j < divisionNum; j++){
IVec pos = particleCurves[i].pt( 1.0/divisionNum*j );
new IParticleTrajectory(pos).fric(0.2).clr(particleCurves[i].clr());
}
}
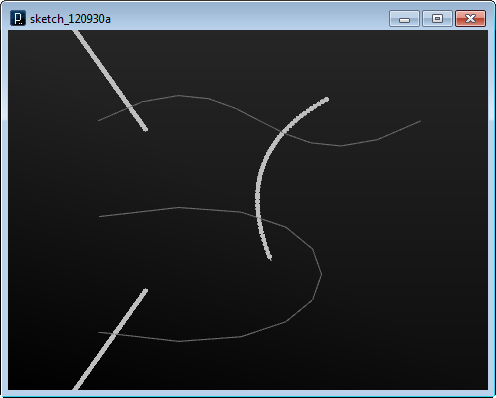

 入力ファイルの曲面とポリゴン・メッシュからのパーティクルの作成
入力ファイルの曲面とポリゴン・メッシュからのパーティクルの作成
多くの箱型のBrepを含むサンプルファイルは以下です。
curve_field_init3.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.duration(250);
IG.darkBG();
IG.open("curve_field_init3.3dm");
ICurve[] fieldCurves = IG.layer("field").curves();
for(int i=0; i < fieldCurves.length; i++){
new ICurveTangentField(fieldCurves[i]).linear(20).intensity(50);
}
IGeometry[] geometries = IG.layer("particle").geometries(); // all geometries in "particle" layer
for(int i=0; i < geometries.length; i++){
new IParticleTrajectory(geometries[i]).fric(0.2); // create a particle out of each geometry
}
以下が初期状態です。

力の場の適用後、それぞれの箱型Brepが力の場に沿って動き回ります。
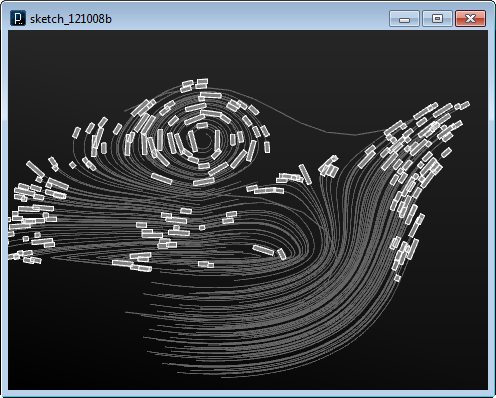
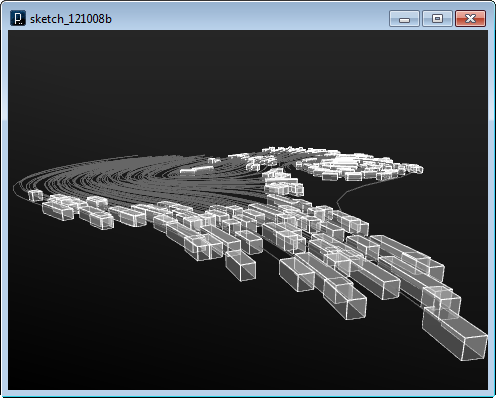
以下のもう一つの例では、 入力の幾何学オブジェクトから、スウォーム・エージェントを生成し、 曲面から生成された力の場を適用します。
以下が例に用いるファイルです。
curve_field_init4.3dm
![]()
![]()
![]()
![]()
import processing.opengl.*;
import igeo.*;
size(480, 360, IG.GL);
IG.darkBG();
IG.duration(700);
IG.open("curve_field_init4.3dm");
ISurface[] fieldSurfaces = IG.layer("field").surfaces();
for(int i=0; i < fieldSurfaces.length; i++){
new I2DSurfaceSlopeField(fieldSurfaces[i]).linear(50).intensity(10);
}
new IFieldVisualizer(-20,-20,0, 20,20,0, 40,40,1);
IGeometry[] geometries = IG.layer("particle").geometries();
for(int i=0; i < geometries.length; i++){
IBoid b = new IBoid(geometries[i]).fric(0.2);
b.cohesionRatio(5.0);
b.cohesionDist(5.5);
b.separationRatio(25.0);
b.separationDist(5.0);
b.alignmentRatio(15.0);
b.alignmentDist(7.0);
}
初期状態。
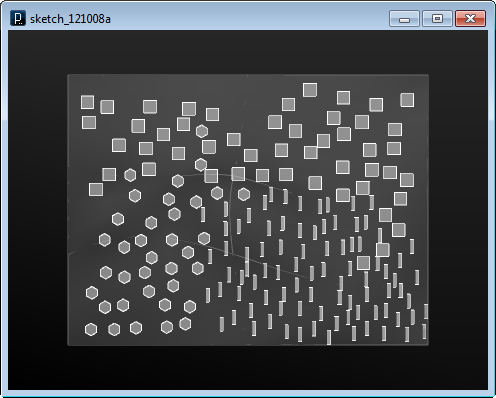
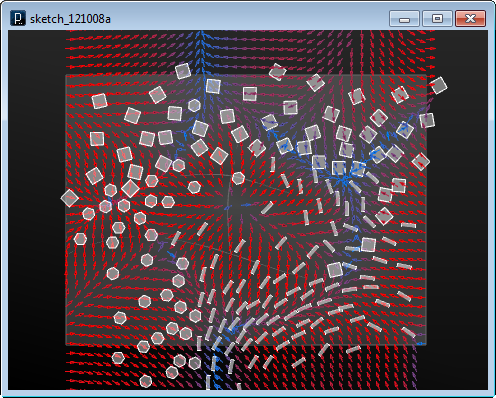
実行後、力の場による勾配場の谷間に集まる様子と、 スウォームの分離規則によって、各々のエージェントが近くなりすぎないように 分散している様子が観察できます。
 HOME
HOME
 FOR PROCESSING
FOR PROCESSING
 DOWNLOAD
DOWNLOAD
 DOCUMENTS
DOCUMENTS
 TUTORIALS (Java /
Python)
TUTORIALS (Java /
Python)
 GALLERY
GALLERY
 SOURCE CODE(GitHub)
SOURCE CODE(GitHub)
 PRIVACY POLICY
PRIVACY POLICY
 ABOUT/CONTACT
ABOUT/CONTACT
